Як підвищити ефективність управління персоналом у рітейлі з урахуванням навантаження на каси

Велика конкуренція у рітейлі мотивує бізнес підвищувати рівень обслуговування своїх клієнтів. Це, перш за все, стосується часу очікування клієнтів, який вони проводять стоячи в черзі на касах. У цьому питанні потрібно знайти баланс оптимальної кількості кас, що забезпечить невеликий обумовлений час очікування в черзі для більшості покупців, і в той же час не призведе до простою кас.

Таку оптимальну кількість кас потрібно розрахувати з дискретністю, яка характерна для бізнесу. Наприклад, у рітейлі це 15-хвилинні інтервали, для яких заздалегідь планується кількість кас, що працюють, по кожній торговій точці.

Навантаження на каси визначається потоком покупців, що виражається у кількості чеків, оброблених за 15-хвилинний інтервал. Навантаження та, відповідно, кількість чеків змінюється протягом доби. Як правило, в рітейлі є два піки – ранковий та вечірній. Також протягом доби може незначно змінюватись середній час обслуговування чека.

У вирішенні поставленого завдання нам допоможе теорія масового обслуговування і, зокрема, завдання, вирішення яких ще на початку XX століття розробив Агнер Краруп Ерланг. Свого часу цей учений був одним із першопрохідників у вивченні теорії телефонного трафіку. Існує сімейство формул Ерланга, якими досі користуються для розрахунків необхідної кількості операторів колл-центру.

У разі рітейлу ми маємо повну аналогію з розрахунками для кол-центру: кількість дзвінків за період відповідає кількості чеків (покупців) за період; середній час обробки дзвінка відповідає середньому часу обробки чека; допустимий час очікування абонента відповідає допустимому часу очікування покупця у черзі; цільовий рівень сервісу – показник, що використовується в обидвих галузях.

Таким чином, загальний підхід для вирішення поставленого завдання виглядає так:

1) Підготовка та обробка даних, які є заголовками чеків, де зафіксовано час відкриття та закриття кожного чека, а також необхідні довідники з торгових точок та кас;

2) Постановка цілей за допустимим часом очікування покупця у черзі та необхідному рівню обслуговування;

3) Прогнозування кількості чеків на майбутній планований період по кожній торговій точці та кожному 15-хвилинному інтервалу;

4) Розрахунок кількості працюючих кас для кожної торгової точки та 15-хвилинного інтервалу відповідно до спрогнозованої кількості чеків та встановлених цілей;

5) Планування змін згідно з отриманими розрахунками для ефективного розподілу ресурсів.

Допустимий час очікування покупця встановлюються бізнесом. Його можна вказати у вигляді розміру черги. Наприклад, допустимий розмір черги 4 особи означає, що 1 людина обслуговується, а 3 особи очікують. У цьому випадку допустимий час очікування в секундах можна визначити множенням 3 на середній час обробки чека.

Цільовий рівень обслуговування також встановлюється бізнесом. Це відсотковий показник, який інтерпретується як “скільки відсотків людей повинні чекати на обслуговування в черзі не довше за допустимий час очікування”. У нормі рівень обслуговування має бути не нижчим за 70, краще за 80%. Важливо розуміти, що 100% рівня сервісу не буває, тому що для цього потрібно повністю виключити затримку при обробці чека.

Важливим та ресурсомістким з погляду обчислень є етап прогнозування кількості чеків. Від точності прогнозування кількості чеків залежить і точність розрахунку необхідної кількості кас, що працюють. Тому модель прогнозування має враховувати безліч чинників, які впливають прогнозований показник та особливості кожної торгової точки. Зокрема, необхідно врахувати мультисезонність (річна, тижнева та денна сезонності), свята, неробочі дні, розташування магазинів. За наявності даних можна закладати у модель додаткові чинники, такі як карантин у навчальних закладах, місцеві свята щодо кожного населеного пункту тощо.

Маючи цільові показники за часом очікування та рівнем обслуговування, знаючи середній час обробки чека та маючи прогнозні значення кількостей чеків розраховуємо рекомендовану кількість кас для кожної торгової точки та часового інтервалу за допомогою формули Ерланг C.

Для аналізу показників, пов’язаних із розрахунками навантаження на каси, було створено BI-додаток. В рамках додатка зручно аналізувати всі вищезазначені показники. Наприклад, отримані результати за прогнозом кількості чеків і необхідної кількості кас, що працюють, доступні як в табличному, так і в графічному вигляді, як показано на малюнку.

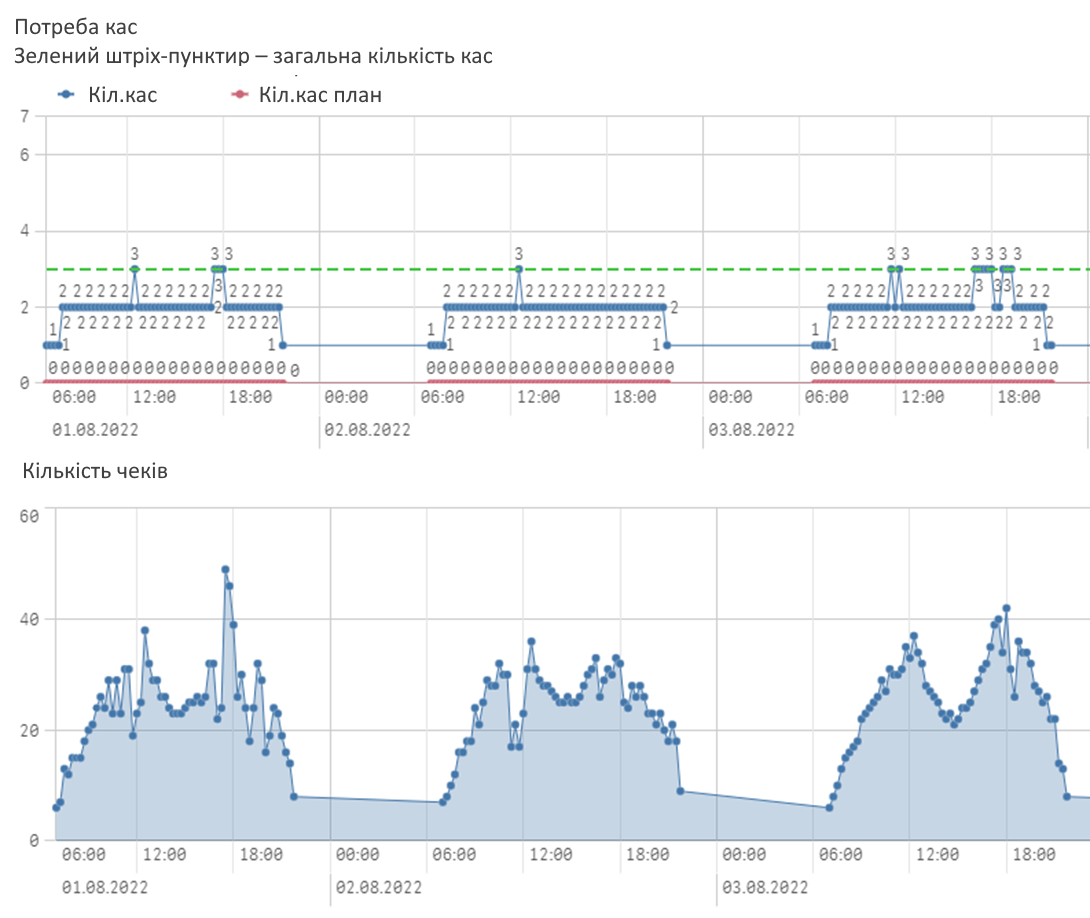
Також у додатку доступний аналіз минулих періодів, котрим вже відоме фактичне навантаження на каси (фактична кількість чеків). У цьому випадку ми порівнюємо три показники: необхідну кількість працюючих кас, розраховану за фактичною кількістю чеків; рекомендована кількість працюючих кас, розрахована за прогнозною кількістю чеків; фактична кількість кас, що працювали. Також є можливість порівнювати рівні обслуговування за фактичною та рекомендованою кількістю працюючих кас.

Викликає цікавість аналіз магазинів що до необхідності додаткової каси і наявності «зайвої» каси. У першому випадку за кожним магазином показано скільки відсотків часу необхідна кількість кас, що працюють, більша, ніж фізична кількість кас у магазині. На підставі цієї інформації менеджер може ухвалити рішення про додавання каси до проблемних магазинів. А в другому випадку за кожним магазином показано скільки відсотків часу є необхідність використання максимальної кількості кас, які є в магазині. Ці два види аналізу також представлені як табличному, і у графічному вигляді.

Таким чином, застосування формул теорії масового обслуговування комплексно з алгоритмами машинного навчання дозволяють успішно вирішувати завдання оптимізації роботи персоналу на касах. Це формує позитивний клієнтський досвід у покупців, допомагає менеджерам приймати рішення щодо планування та розподілу ресурсів, а також економить людино-години персоналу, який може працювати в залі, замість того, щоб пересиджувати на касі.